Why and How to Use Behavior Trees in Your Robot Application?

29 Jun, 2025

Say you want your robot to perform a complex behavior like "bring me a glass of water," "go water the plants," or "make a sandwich in the kitchen." How do you even begin to program that? You could write a labyrinth of if-else statements, build a tangled web of state machines, or you could use a more modular and intuitive approach: Behavior Trees (BTs in short).

BTs are used to create complex behaviors from simple, reusable building blocks. Think of it as a layer of abstraction that sits on top of the low-level actions your robot can perform. You're not just telling the robot what to do; you're also orchestrating how and when to do it in a structured way.

Because they are hierarchical in nature, these building blocks, or "behaviors," can themselves be composed of smaller behavior trees.

For example, a task like RechargeBattery could be a high-level behavior. This BT would orchestrate a series of smaller actions: CheckBatteryLevel, BlinkWarningLights, MoveToChargingStation, and ChargeBattery. Each of these actions can be broken down even further if needed, creating a clear, hierarchical structure that's easy to understand, debug, and expand.

What Does a Behavior Tree Look Like?

As the name suggests, it's a tree. It has a root, and nodes branch out from there. Execution always starts at the root and follows a specific path down the branches, from left to right. This process is called "ticking," and it continues until it reaches a leaf node that returns a Terminal State: SUCCESS or FAILURE.

Leaf Nodes are the ones that do the actual work. A leaf node's task could be a simple check or a more complex action. So naturally, leaf nodes are the places where you connect the behavior tree to the lower-level code for your specific application.

Internal nodes in the tree are responsible for controlling the tree traversal. Each internal (non-leaf) node of the tree will accept the resulting status of its children (like SUCCESS, FAILURE, or RUNNING) and then decide what to do next and which node to visit next.

So how are BTs executed?

They are 'ticked' at a specified rate. Ticking means that the tree is traversed from the root node to the child nodes recursively. After any node is ticked, it returns a status to its parent, which can be SUCCESS, FAILURE, or RUNNING.

Terminology of a Behavior Tree

Before we proceed, let's understand the terminology used in BT literature. To be able to use external libraries like BT.CPP or go over the tree designs of other people, you need to speak the same language before you can understand the design.

A BT is made up of different types of nodes, but they fall into two main categories:

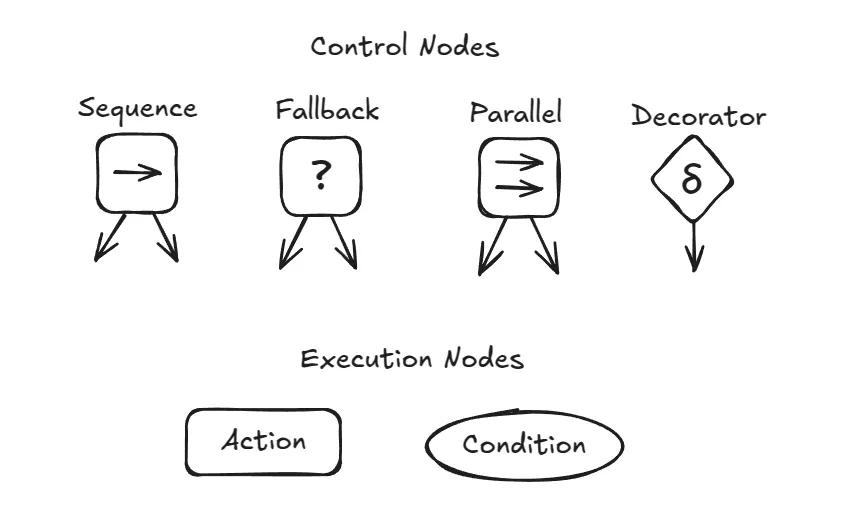
• Execution Nodes: These are the leaves of the tree, and they perform the actual work. When ticked, an execution node performs its task and returns a status:

  • SUCCESS: The task was completed successfully.
  • FAILURE: The task could not be completed.
  • RUNNING: The task is still in progress (e.g., navigating to a location).

• Control Flow Nodes: These are the internal nodes of the tree. Their job is to control the flow of execution. They tick their children in a specific order and, based on the status they receive back, decide which node to tick next.

Control nodes can have other control nodes as children.

To build our own BTs, we'll need to understand a few common node types, especially those used in popular libraries like BehaviorTree.CPP (or BT.CPP for short).

The Two Types of Execution Nodes

As mentioned earlier, execution nodes are where the action happens. They have two types:

• Condition Nodes: These are for quick checks. They execute in a single tick and return either SUCCESS or FAILURE, like checking IsGripperOpen? or IsBatteryLow?. They check a state and immediately report back.

• Action Nodes: These represent tasks that might take time to complete. An action like OpenDoor or NavigateToPose might span multiple ticks. While the task is ongoing, the node returns RUNNING. Once it's done, it returns SUCCESS or FAILURE.

The Essential Control Flow Nodes

Control nodes are the internal nodes of the BT. They decide how to traverse the BT given the status of their children. Now, the children of Control nodes can be execution nodes or other control nodes, which is why this is a hierarchical structure.

The Sequence, Fallback, and Parallel nodes can have any number of children, but what differs is how they process the status of their children.

Decorator nodes necessarily have one child and modify its behavior with some custom user-defined logic.

Let's go over them in a bit more detail.

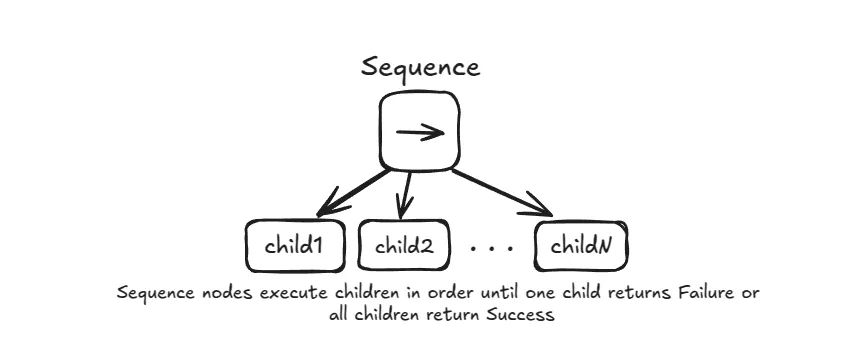
• Sequence (→): Ticks its children in order from left to right.
  • If a child returns FAILURE, the Sequence node stops and immediately returns FAILURE.
  • If a child returns SUCCESS, it ticks the next child in the sequence.
  • If all children return SUCCESS, the Sequence node returns SUCCESS.
  • It's for tasks where the order of operations matters, like "first open the door, then move through it."

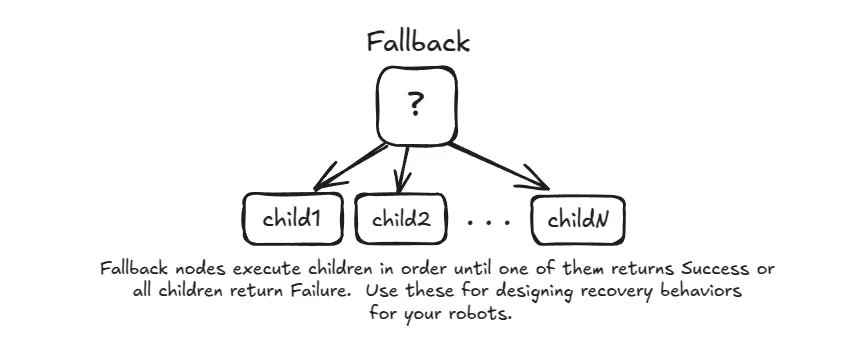
• Fallback (?): Ticks its children in order until one returns SUCCESS.
  • If a child returns SUCCESS, the Fallback node stops and immediately returns SUCCESS.
  • If a child returns FAILURE, it moves to the next child to try an alternative.
  • If all children return FAILURE, the Fallback node returns FAILURE.
  • It's perfect for creating backup plans, like "try picking up the cup with the right arm; if that fails, try with the left arm."

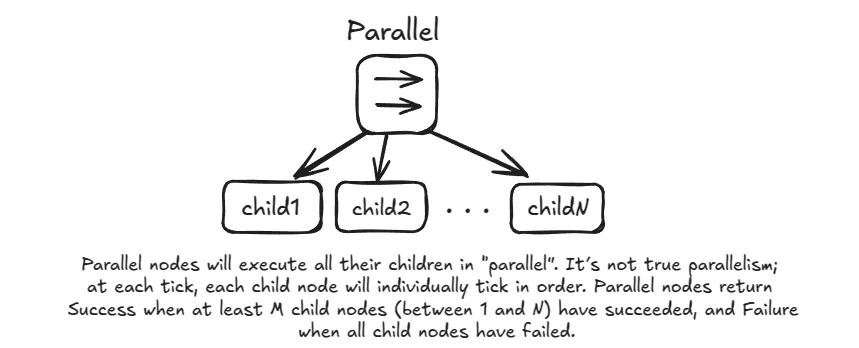
• Parallel (⇉): Ticks all of its children. It returns SUCCESS or FAILURE based on a configurable policy (e.g., return SUCCESS if M out of N children succeed). This is useful for tasks that should happen at the same time, like DriveForward while simultaneously running CheckForObstacles.

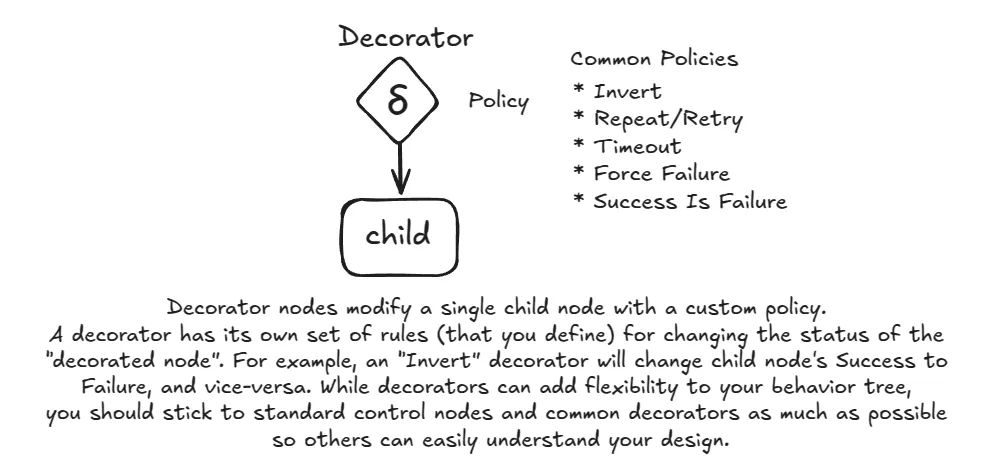
• Decorator Nodes: These are special control nodes that have only one child. Their purpose is to modify the behavior of that child. For example, an Inverter decorator will invert the result of its child (turning SUCCESS into FAILURE and vice-versa). A Retry decorator will re-tick its child a specified number of times if it fails.

Let's Get Our Hands Dirty

Theory is great, but the best way to understand is to build something. Let's create a BT for a mobile robot tasked with finding a colored box in a room.

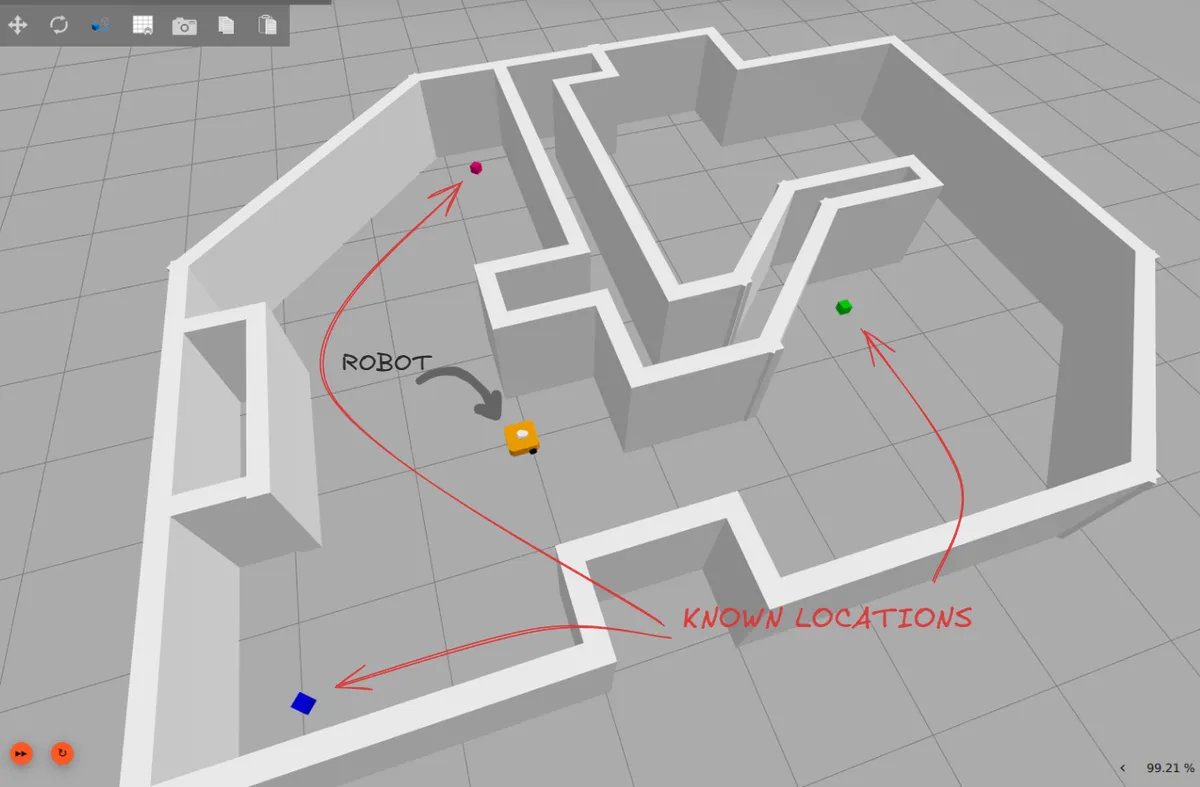
The Scenario: Our robot operates in a known environment. We have a few predefined locations where a box might be. The robot needs to navigate to these locations, one by one, and use its camera to check if the box at that location is the color we're looking for.

• Goal: Find the box with the correct color.
• Actions: Navigate to a location, perform a visual check.
• Logic: If the box is found, the mission is a SUCCESS. If not, move to the next location and try again.

To begin designing a BT, let's start with the simplest case: visiting just one location. The logic is straightforward: "Go to Location 1, then look for the box." This is a perfect job for a Sequence node.

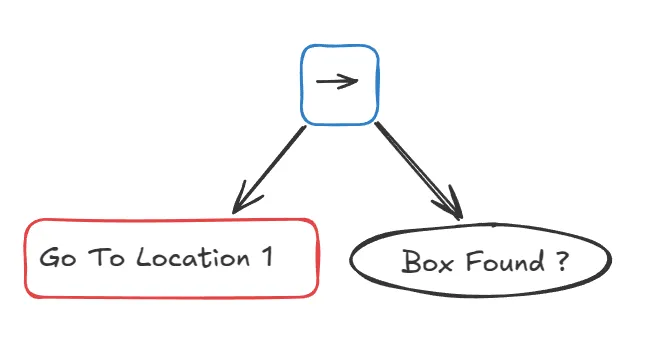
Our Go To Location 1 action might take time, so it will return RUNNING while the robot is moving and SUCCESS upon arrival. Once we get SUCCESS from the Go To Location 1 action, we can check if the box is found. The Box Found? action is a quick condition: it returns SUCCESS if the right box is seen, FAILURE otherwise.

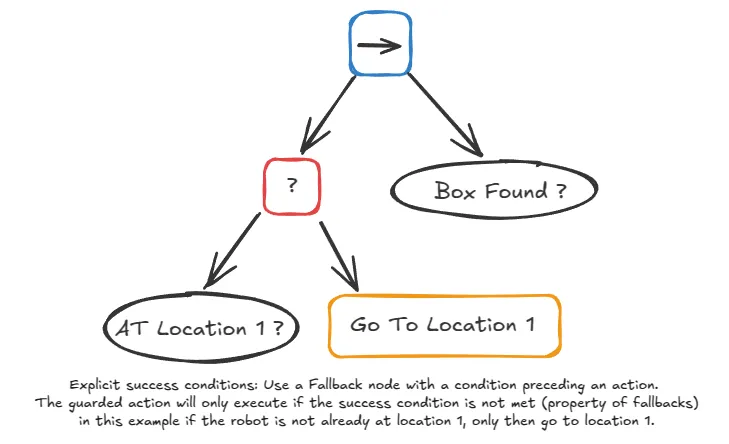
A quick note on good BT design: always check before you act. This principle of "explicit success conditions" makes your trees more robust. For example, instead of just assuming a navigation command worked, a better sequence would be to first check if the robot is at the location (At Location 1?), if not, Go To Location 1, and then check if the box is found (Box Found?). This confirms each step's success before proceeding.

Scaling Up: What About Multiple Locations?

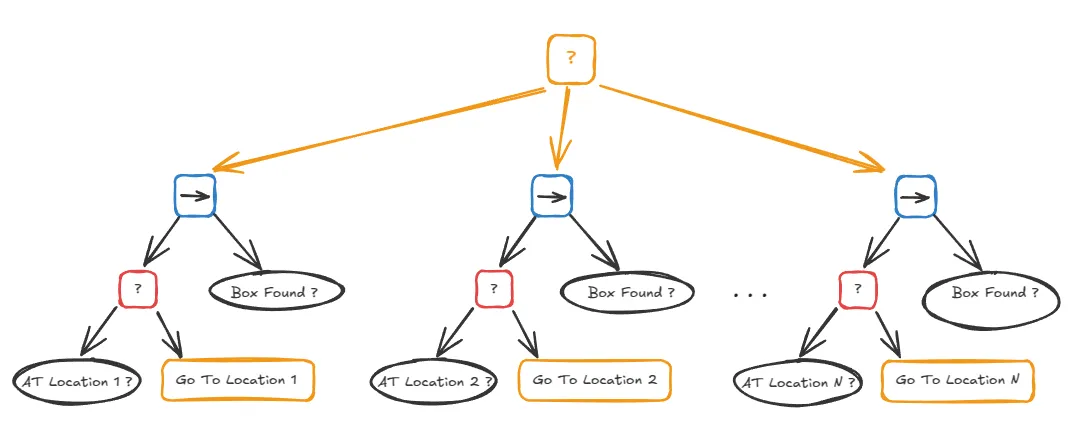
Now, how do we handle searching in multiple locations? As shown in the image above, we can build a giant tree with a fallback node at the root and a separate sequence for each location, but that's inefficient and hard to maintain. If we had 100 locations, that approach would be a nightmare.

Here, the tree will try the first branch: the sequence for "Go to Location 1 & Check". If that sequence fails (meaning the box wasn't found), the Fallback moves to the next child and tries the sequence for "Go to Location 2 & Check", and so on. The entire tree succeeds as soon as one of the search sequences finds the box.

This is quite inefficient, but before we design a smarter solution, let's discuss the concept of the blackboard briefly.

Sharing Data Between Nodes: The Blackboard

What if we could give the robot a list of locations and have it visit them one by one? To do that, nodes need a way to share information. This is where the Blackboard comes in.

The Blackboard is a shared key-value storage area that all nodes in a tree can access. One node can write a piece of data (like a list of coordinates) to the blackboard, and other nodes can read it.

• Output Port: A node uses this to write data to a key on the blackboard.
• Input Port: A node uses this to read data from a key on the blackboard.

Now we can design our final solution.

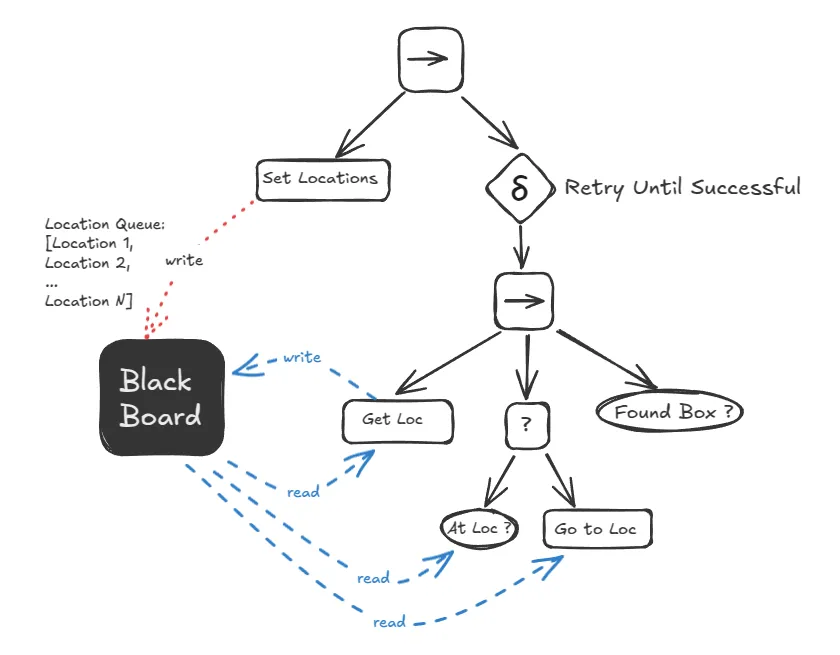
In this design:

1. The root is a Sequence node. Its first job is to run a SetLocations action, which populates the blackboard with a queue of all the search locations. This runs only once.
2. Next, a RetryUntilSuccessful decorator is ticked. This decorator will continuously tick its child until it returns SUCCESS.
3. The child is another Sequence that performs the core loop:
   • GetNextLocation: Pops a location from the queue on the blackboard.
   • NavigateTo: Moves the robot to that location.
   • CheckForObject: Looks for the box.
4. If the box is found, the inner sequence succeeds, the Retry decorator succeeds, and the whole tree finishes. If not, the sequence fails, and the Retry decorator tries the loop again with the next location.

Regular vs. Reactive Behavior

One last concept to touch on is the difference between a regular Sequence and a Reactive Sequence.

In a regular Sequence, once a child node returns SUCCESS, the tree considers it "done" and doesn't tick it again in subsequent tree updates. It moves on to the next child.

A Reactive Sequence, however, re-ticks all its children on every update, starting from the first one, regardless of their previous status.

Why does this matter? Imagine you have a condition like IsBatteryLow? at the start of a long sequence of actions. With a regular sequence, the battery would be checked once, and even if it became low later, the tree wouldn't know because that node is never re-ticked. With a Reactive Sequence, the battery status would be checked on every single tick, allowing the robot to immediately react to a critical change in its state.

Visit the Github Repo

To test and run this example yourself, you can visit the Github Repo and follow the instructions to build and run the example.

References

• Behavior Trees in Robotics and AI: An Introduction
• Introduction to Behavior Trees
• Behavior Tree CPP